用一行 list comprehension 解魔方陣

小朋友的學校給了一個特殊的魔方陣題目，基本上用列舉的方式，每一種可能發生的狀況慢慢列出來，然後排除不合理的狀況，就可以得出結果了。

題目：
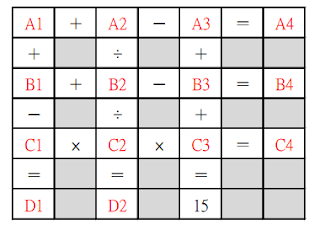
空格是 1~14 正整數，數字不會重複出現，且要滿足直與橫的運算式。（我把空格都先加上了變數名稱）

A1 + A2 - A3 = A4
B1 + B2 - B3 = B4
C1 * C2 * C3 = C4

A1 + B1 - C1 = D1
A2 / B2 / C2 = D2
A3 + B3 + C3 = 15

計算：
如果要直接算，應該可以用 1 ~ 14 每個數字的正因數列表，來列出 A2 / B2 / C2 = D2 的所有狀況，另外再列出 A3 + B3 + C3 = 15 的所有狀況，然後再搭配 C1 C2 C3 = C4 應該就能找出解答。

不過我沒耐心慢慢去列舉，就想到其實列舉，並滿足某個條件，正是 list comprehension 最強大的用途。

第一版

L=[{A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,D1,D2}||
     A1 <- lists:seq(1,14),
     A2 <- lists:seq(1,14),
     A3 <- lists:seq(1,14),
     A4 <- lists:seq(1,14),

     B1 <- lists:seq(1,14),
     B2 <- lists:seq(1,14),
     B3 <- lists:seq(1,14),
     B4 <- lists:seq(1,14),

     C1 <- lists:seq(1,14),
     C2 <- lists:seq(1,14),
     C3 <- lists:seq(1,14),
     C4 <- lists:seq(1,14),

     D1 <- lists:seq(1,14),
     D2 <- lists:seq(1,14),

     A1=/=A2,
     A2=/=A3,
     A3=/=A4,
     A4=/=B1,
     B1=/=B2,
     B2=/=B3,
     B3=/=B4,
     B4=/=C1,
     C1=/=C2,
     C2=/=C3,
     C3=/=C4,
     C4=/=D1,
     D1=/=D2,
     D2=/=A1,

     A1+A2-A3=:=A4,
     B1+B2-B3=:=B4,
     C1*C2*C3=:=C4,
     A1+B1-C1=:=D1,
     (A2 div B2) div C2=:=D2,
     A3+B3+C3=:=15
    ].

跑了幾分鐘還沒得到結果，所以就停掉，改第二版

K = lists:seq(1,14).
L=[{A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,D1,D2}||
     A1 <- K,
     A2 <- K--[A1],
     A3 <- K--[A1,A2],
     A4 <- K--[A1,A2,A3],

     B1 <- K--[A1,A2,A3,A4],
     B2 <- K--[A1,A2,A3,A4,B1],
     B3 <- K--[A1,A2,A3,A4,B1,B2],
     B4 <- K--[A1,A2,A3,A4,B1,B2,B3],

     C1 <- K--[A1,A2,A3,A4,B1,B2,B3,B4],
     C2 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1],
     C3 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2],
     C4 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3],

     D1 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4],
     D2 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,D1],

     A1+A2-A3=:=A4,
     B1+B2-B3=:=B4,
     C1*C2*C3=:=C4,
     A1+B1-C1=:=D1,
     (A2 div B2) div C2=:=D2,
     A3+B3+C3=:=15
    ].

等了很久還是沒結果，判斷應該是前面列舉出來的結果太多了，改第三版

K = lists:seq(1,14).
L=[{A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,D1,D2}||
     A1 <- K,
     A2 <- K--[A1],
     A3 <- K--[A1,A2],
     A4 <- K--[A1,A2,A3],
     A1+A2-A3=:=A4,

     B1 <- K--[A1,A2,A3,A4],
     B2 <- K--[A1,A2,A3,A4,B1],
     B3 <- K--[A1,A2,A3,A4,B1,B2],
     B4 <- K--[A1,A2,A3,A4,B1,B2,B3],
     B1+B2-B3=:=B4,

     C1 <- K--[A1,A2,A3,A4,B1,B2,B3,B4],
     C2 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1],
     C3 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2],
     C4 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3],
     C1*C2*C3=:=C4,

     D1 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4],
     D2 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,D1],

     A1+B1-C1=:=D1,
     (A2 div B2) div C2=:=D2,
     A3+B3+C3=:=15
    ].

測試結果

1> test:resolve().
[{7,14,8,13,10,4,5,9,6,1,2,12,11,3},
 {8,12,7,13,11,4,6,9,5,1,2,10,14,3}]

答案有兩組，但實際上驗算，會發現整數除法有問題，第一組答案是錯的。

因此，我們再加上一個條件，來排除整數除法的問題。

D2*C2*B2=:=A2

這就行了，最終再加上計算的時間統計

resolve() ->
    statistics(runtime),
    statistics(wall_clock),
    K = lists:seq(1,14),
    L=[{A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,D1,D2}||
     A1 <- K,
     A2 <- K--[A1],
     A3 <- K--[A1,A2],
     A4 <- K--[A1,A2,A3],
     A1+A2-A3=:=A4,

     B1 <- K--[A1,A2,A3,A4],
     B2 <- K--[A1,A2,A3,A4,B1],
     B3 <- K--[A1,A2,A3,A4,B1,B2],
     B4 <- K--[A1,A2,A3,A4,B1,B2,B3],
     B1+B2-B3=:=B4,

     C1 <- K--[A1,A2,A3,A4,B1,B2,B3,B4],
     C2 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1],
     C3 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2],
     C4 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3],
     C1 * C2 * C3=:=C4,

     D1 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4],
     D2 <- K--[A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,D1],

     A1+B1-C1=:=D1,
     (A2 div B2) div C2=:=D2,
     D2*C2*B2=:=A2,
     A3+B3+C3=:=15
    ],
    {_, Time1} = statistics(runtime),
    {_, Time2} = statistics(wall_clock),
    io:format("runtime=~p wall_clock=~p ~n", [Time1, Time2]),
    L.

測試結果

1> test:resolve().
runtime=96284 wall_clock=104801
[{8,12,7,13,11,4,6,9,5,1,2,10,14,3}]

最後答案就是

===========

原本的計算時間花太久了，今天想到應該要先計算這兩個式子，才能有效在前面就把篩選的可能狀況減少

A2 / B2 / C2 = D2
C1 * C2 * C3 = C4

再修改程式，首先把 =:= 完全相等 換成 == 邏輯相等，也不用整數除法 div，改為 / ，接下來再調整運算的順序。

resolve() ->
    statistics(runtime),
    statistics(wall_clock),
    K = lists:seq(1,14),
    L=[{A1,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,D1,D2}||
       A2 <- K,
       B2 <- K--[A2],
       C2 <- K--[A2,B2],
       D2 <- K--[A2,B2,C2],
       (A2 / B2) / C2==D2,

       C1 <- K--[A2,B2,C2,D2],
       C3 <- K--[A2,B2,C2,D2,C1],
       C4 <- K--[A2,B2,C2,D2,C1,C3],
       C1*C2*C3==C4,

       A3 <- K--[A2,B2,C2,D2,C1,C3,C4],
       B3 <- K--[A2,B2,C2,D2,C1,C3,C4,A3],
       A3+B3+C3==15,

       A1 <- K--[A2,B2,C2,D2,C1,C3,C4,A3,B3],
       A4 <- K--[A2,B2,C2,D2,C1,C3,C4,A3,B3,A1],
       A1+A2-A3==A4,

       B1 <- K--[A2,B2,C2,D2,C1,C3,C4,A3,B3,A1,A4],
       B4 <- K--[A2,B2,C2,D2,C1,C3,C4,A3,B3,A1,A4,B1],
       B1+B2-B3==B4,

       D1 <- K--[A2,B2,C2,D2,C1,C3,C4,A3,B3,A1,A4,B1,B4],
       A1+B1-C1==D1
      ],
    {_, Time1} = statistics(runtime),
    {_, Time2} = statistics(wall_clock),
    io:format("runtime=~p wall_clock=~p ~n", [Time1, Time2]),
    L.

測試結果很驚人，花掉的時間變得非常短。

1> test:resolve().
runtime=0 wall_clock=0
[{8,12,7,13,11,4,6,9,5,1,2,10,14,3}]
2> test:resolve().
runtime=15 wall_clock=15
[{8,12,7,13,11,4,6,9,5,1,2,10,14,3}]

結論，寫程式還是需要 follow 手算的想法，好的演算法，才能有效減少電腦計算的時間。