確認模型的正確性,針對建立的模型,以評估的方法進行機器學習。
迴歸與分類都是定義預測時所需要的函數 \(f_𝜃(x)\),藉由學習資料來找到函數中的 𝜃。方法是將目標函數進行微分,求得參數更新式。但實際上需要的,是預測函數得到的預測值,例如花多少廣告費可得多少點擊率。
我們需要量測函數 \(f_𝜃(x)\) 的正確性(精確度),但像多元迴歸,無法用圖形表示,就需要將機器學習的模型的精度,以定量的方式表示,然後表現其精確度,這就是模型評估。因為參數是透過學習資料修正而來的,對於原本的學習資料來說,參數是正確的,但對於新的資料就不一定了。
交叉驗證 Cross Validation
將學習資料區分為學習以及測試使用,用測試用的資料評估模型,一般來說,學習用的資料會比較多。
在回歸問題中,函數 \(f_𝜃(x)\) 是透過習資料修正而來的,對於原本的學習資料來說,參數是正確的,但對於測試部分的資料就不一定正確了。
假設測試資料有 n 筆,將測試用的資料,透過模型求得結果,再跟原本的實際值比較得到誤差。以下為均方差 MSE (Mean Square Error)
\( \frac{1}{n} \sum_{i=1}^{n} ( y^{(i)} - f_𝜃(x^{(i)} ) )^2 \)
當均方差越小,表示模型的精度很高。
分類問題的驗證
因迴歸問題是連續值,可用誤差進行驗證,分類問題是邏輯迴歸,回到矩形是橫向或縱向的問題上,會有四種狀況。
| 分類結果 | 原本是橫向 | 原本是縱向 |
|---|---|---|
| 橫向 | 正確 | 錯誤 |
| 縱向 | 錯誤 | 正確 |
可將二元分類轉換為這樣的表格
| 分類結果 | + | - |
|---|---|---|
| + Positive | True Positive (TP) | False Positive (FP) |
| - Negative | False Negative (FN) | True Negative (TN) |
分類的精度,就是在全部的資料中,能夠被正確分類的 TP與 TN 佔的比例,可表示為
\( Accuracy = \frac{TP + TN}{TP+FP+FN+TN} \)
ex: 100 筆測試資料,有 80 筆正確
\( Accuracy = \frac{80}{100} = 0.8\)
精確率與回現率
有時候只用精確度評估分類結果會遇到問題。例如當原始資料有大量資料 95 筆為 Negative,只有一點點資料 5 筆為 Positive,如果將全部測試資料都分類為 False 的模型,Accuracy 為 0.95,精確度很高但實際上這是一個錯誤的預測模型。
因此要導入其他評估的指標。
精確率 Precision: 分類為 Positive 的資料中,實際為 Positive 的資料數的比例。值越高,代表分類錯誤的越少。
\( Precision = \frac{TP}{TP+FP}\)
回現率 Recall: Positive 資料中,實際上分類為 Positive 的資料數。值越高,代表沒有被遺漏,且被正確分類的比例。
\( Recall = \frac{TP}{TP+FN} \)
通常精確率與回現率,只要有ㄧ個是高的,另一個就會變低。
舉例來說,
| 資料 | 個數 |
|---|---|
| Positive | 5 |
| Negative | 95 |
| 評估結果 | |
| True Positive | 1 |
| False Positive | 2 |
| False Negative | 4 |
| True Negative | 93 |
| 精確度 Accuracy | 94% |
| 精確率 Precision | \(\frac{1}{1+2} = 0.333\) |
| 回現率 Recall | \(\frac{1}{1+4} = 0.2\) |
F 值 (Fmeasure)
通常精確率與回現率,只要有ㄧ個是高的,另一個就會變低。但直接將兩個平均,也不是好的指標
| 模型 | 精確率 | 回現率 | 平均 |
|---|---|---|---|
| A | 0.6 | 0.39 | 0.495 |
| B | 0.02 | 1.0 | 0.51 |
B 模型是將全部的資料都分類為 Positive,但因為 Negative 也分類為 Positive,所以精確率很低,實際上,B 不是一個好的模型。
Fmeasure 定義如下,只要 Precision 或 Recall 其中一項變低,就會影響到 Fmeasure
\( Fmeasure = \frac{2}{ \frac{1}{Precision} + \frac{1}{Recall} } = \frac{2 \cdot Precision \cdot Recall}{Precision + Recall}\)
| 模型 | 精確率 | 回現率 | 平均 | Fmeasure |
|---|---|---|---|---|
| A | 0.6 | 0.39 | 0.495 | 0.472 |
| B | 0.02 | 1.0 | 0.51 | 0.039 |
F值有時被稱為 F1 值
F值可再加上權重
\(WeightedFmeasure = \frac{ (1+𝛽)^2 \cdot Precision \cdot Recall }{ 𝛽^2 \cdot Precision + Recall }\)
將權重設定為 1 就是原本的 F 值,也就是 F1值
剛剛都是以 TP 為主,考慮精確率與回現率。如果以 TN 為主
\( Precision = \frac{TN}{TN+FN} \)
\( Recall = \frac{TN}{TN+FP} \)
當測試資料 Positive 的部分較少,就用 Positive 的 Precision, Recall 來評估。
交叉驗證中,以 K 等分交叉驗證最常見
- 將學習資料分為 K 筆
- K-1 筆作為學習用的資料,1 筆作為測試資料
- 將學習用資料與測試資料,一邊交換,一邊驗證,重複 K 次交叉驗證
- 最後計算 K 筆精度平均值,視為最終的精度
例如 4 等分
正規化
過適 Overfitting
只跟學習資料吻合的狀態就是 overfitting。如果迴歸中 \(f_𝜃(x)\) 的次方數過度增加,就會造成 overfitting。分類有一樣的問題。
為了避免 overfitting,有以下對應方式
- 增加學習資料的數量
- 將模型簡化為較簡單的形式
- 正規化
正規化
在迴歸分析中的誤差函數為
\({E(𝜃)= \frac{1}{2} \sum_{i=1}^{n}( y^{(i)} - f_𝜃(x^{(i)})^2 }\)
對該目標函數,再增加正規化的項目 \(R(𝜃) = \frac{𝜆}{2} \sum_{j=1}^{m} 𝜃_j^2\)
\({E(𝜃)= \frac{1}{2} \sum_{i=1}^{n}( y^{(i)} - f_𝜃(x^{(i)})^2 } + R(𝜃)\)
對新的目標函數進行最小化,就是正規化
m 是參數的個數,通常對於 \(𝜃_0\) 來說,無法做正規化,只能從 j=1 開始。例如 \(f_𝜃(x) = 𝜃_0 + 𝜃_1x + 𝜃_2x^2\) 中,m 為 2,正規化的參數對象為 \(𝜃_1, 𝜃_2\)。\(𝜃_0\) 被稱為 bias 項
𝜆 是決定對於正規化項的影響為正的常數,要自己決定用什麼值。
正規化的效果
先將目標函數分為兩項
\( C(𝜃)= \frac{1}{2} \sum_{i=1}^{n}( y^{(i)} - f_𝜃(x^{(i)})^2 \)
\(R(𝜃) = \frac{𝜆}{2} \sum_{j=1}^{m} 𝜃_j^2\)
因為 C(𝜃) 假設是任意一個曲線,R(𝜃) 是二次函數,任意假設它為 \( \frac{1}{2} 𝜃_1^2\) ,是通過原點的二次函數
正規化後,\(𝜃_1\) 最小值會往原點靠近
\( f_𝜃(x) = 𝜃_0 + 𝜃_1x+ 𝜃_2x^2 \) 是二次曲線,但如果 \( 𝜃_2 \) 為 0,變成一次直線,就簡化了模型
𝜆 的大小,決定正規化的影響,如果 \( 𝜆=0 \) 就等於沒有用到正規化
分類的正規化
分類問題是用對數似然函數
\(\log L(𝜃) = \log \prod _{i=1}^{n} P( y^{(i)} = 1|x^{(i)} )^{y^{(i)}} P( y^{(i)} = 0|x^{(i)} )^{1-y^{(i)}}\)
正規化就是再加上 R(𝜃) 的部分,另外因為對數似然指數,原本是要最大化,為了轉換為最小化,加上負號
\(\log L(𝜃) = - \log \prod _{i=1}^{n} P( y^{(i)} = 1|x^{(i)} )^{y^{(i)}} P( y^{(i)} = 0|x^{(i)} )^{1-y^{(i)}} + \frac{𝜆}{2} \sum_{j=1}^{m}𝜃_j^2\)
正規化後的微分
因為 \( E(𝜃) = C(𝜃) + R(𝜃) \) ,就分別對 C(𝜃), R(𝜃) 進行偏微分
\(\frac{𝜕C(𝜃)}{𝜕𝜃_j} = \sum_{i=1}^{n}( f_𝜃(x^{(i)} )-y^{(i)} )x_j^{(i)} \)
\(R(𝜃) = \frac{𝜆}{2} \sum_{j=1}^{m} 𝜃_j^2 = \frac{𝜆}{2}𝜃_1^2 + \frac{𝜆}{2}𝜃_2^2 + \cdots + \frac{𝜆}{2}𝜃_m^2 \)
\( \frac{𝜕R(𝜃)}{𝜕𝜃_j} = 𝜆𝜃_j\)
因此參數更新式就改為
\(𝜃_j := 𝜃_j - 𝜂 ( \sum_{i=1}^{n}( f_𝜃(x^{(i)} )-y^{(i)} )x_j^{(i)} + 𝜆𝜃_j )\)
關於 \(𝜃_0\) 的部分,無法處理正規化,因為 R(𝜃) 以 \(𝜃_0\) 微分後變成 0
邏輯迴歸是類似的過程
E(𝜃) = C(𝜃) + R(𝜃)
\(\log L(𝜃) = - \log \prod _{i=1}^{n} P( y^{(i)} = 1|x^{(i)} )^{y^{(i)}} P( y^{(i)} = 0|x^{(i)} )^{1-y^{(i)}} + \frac{𝜆}{2} \sum_{j=1}^{m}𝜃_j^2\)
\(R(𝜃) = \frac{𝜆}{2} \sum_{j=1}^{m} 𝜃_j^2\)
微分後,因為 R(𝜃) 以 \(𝜃_0\) 微分後變成 0
\(𝜃_0:= 𝜃_0 - 𝜂 ( \sum_{i=1}^{n}( f_𝜃(x^{(i)}) - y^{(i)} )x_j^{(i)} ) \)
\(𝜃_j := 𝜃_j - 𝜂 ( \sum_{i=1}^{n}( f_𝜃(x^{(i)}) - y^{(i)} )x_j^{(i)} + 𝜆𝜃_j ) \quad\quad\quad j > 0 \)
正規化不是只有一種,目前都是 L2 正規化。 L1正規化,用在判斷非必要的參數,會變成0,用來減少變數的數量。L1 正規化是要減少不必要的變數,L2 正規化是要抑制變數的影響。
學習曲線
乏適 Underfitting
跟 Overfitting 相反的狀況是 Underfitting,也就是找不到適合學習資料的模型。
光只有查看精度,沒辦法判斷是 overfitting 或是 underfitting
以這個圖形為例,看起來學習資料是二次曲線,很難找到一條一次函數的直線,適合這些學習資料,隨著學習資料變多,模型的精度會一直下降
使用學習資料數量較少的模型,去預測未知資料會比較困難,精度會比較低。如果學習資料越多,精度會增加。
將學習用資料與測試用資料數量,及精度的對照,繪製圖表。
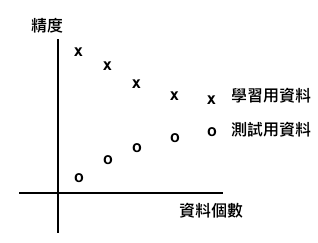
如出現高偏差的狀況,對學習資料數量增加,但精度降低,測試資料增加,精度會增加,且兩個精度會越來越接近。這種狀況就是 underfitting
如果發現有高方差的狀況,就是對學習資料數量增加,但精度一直維持很高,測試資料增加,卻沒辦法增加精度。這種狀況就是 overfitting
這種將資料個數與精度繪製的圖表,就稱為學習曲線。




沒有留言:
張貼留言